常见的排序算法与实现(PHP)汇总
- 冒泡排序
- 选择排序
- 插入排序
- 快速排序
- 归并排序
- 堆排序
- 桶排序
- 基数排序
- 希尔排序
冒泡排序
思路分析
在排序的一组数中,对当前还未排好的序列,从前后对相邻的两个数依次进行比较和调整,让较大的数往下沉,较小的数往上冒。
即,每当两个相邻的数比较后发现它们的排序与排序要求相反时,就将它们互换。
实现
<?php
$arr = array(1,223,23,43,54,455,26,823,45,9,23,65);
/**
* [bubblingSort description]
* @param [type] $arr [description]
* @return [type] [description]
*/
function bubblingSort($arr){
$len = count($arr);
//控制需要冒泡的轮数
for($i = 1;$i < $len; $i++){
//控制每层冒出一个数 需要比较的次数
for($k = 0; $k < $len-$i; $k++){
if($arr[$k] > $arr[$k+1]){
$temp = $arr[$k+1];
$arr[$k+1] = $arr[$k];
$arr[$k] = $temp;
}
}
}
return $arr;
}
var_dump(bubblingSort($arr));
选择排序
思路分析
在要排序的一组数中,选出最小的一个数与第一个位置的数交换。
然后在剩下的数当中再找最小的与第二个位置的数交换,如此循环到倒数第二个数和最后一个数比较为止。
实现
<?php
$arr = array(1,223,23,43,54,455,26,823,45,9,23,65);
/**
* [selectSort description]
* @param [type] $arr [description]
* @return [type] [description]
*/
function selectSort($arr){
//双重循环,外层控制循环轮数,内层控制比较次数
$len = count($arr);
for($i=0;$i<$len-1;$i++){
//先假设最小的值的位置
$p = $i;
for($j=$i+1;$j<$len;$j++){
//$arr[$p] 是当前已知的最小值
if($arr[$p] > $arr[$j]){
//比较,发现更小的,记录下最小值的位置;并且在下次比较时采用已知的最小值进行比较
$p = $j;
}
}
//已经确定了当前的最小值的位置,保存到$p中。如果发现最小值的位置与当前假设的位置$i不同,则位置互换即可。
if($p != $i){
$tmp = $arr[$p];
$arr[$p] = $arr[$i];
$arr[$i] = $tmp;
}
}
return $arr;
}
var_dump(selectSort($arr));
插入排序
思路分析
在要排序的一组数中,假设前面的数已经是排好顺序的,现在要把第n个数插入到前面的有序数中,使得这n个数也是排好序的。如此反复循环,直到全部排好顺序。
实现
<?php
$arr = array(1,223,23,43,54,455,26,823,45,9,23,65);
/**
* [insertSort description]
* @param [type] $arr [description]
* @return [type] [description]
*/
function insertSort($arr){
$len = count($arr);
for($i=1;$i<$len;$i++){
$tmp = $arr[$i];
//内层循环控制,比较并插入
for($j=$i-1;$j>=0;$j--){
if($tmp < $arr[$j]){
//发现插入的元素要小,交换位置,将后边的元素与前面的元素互换
$arr[$j+1] = $arr[$j];
$arr[$j] = $tmp;
} else{
//如果碰到不需要移动的元素,由于是已经排序好的数组,则前面的就不需要再次比较了
break;
}
}
}
return $arr;
}
var_dump(insertSort($arr));
快速排序
思路分析
选择一个基准元素,通常选择第一个元素或者最后一个元素。通过一趟扫描,将待排序列分成两部分,一部分比基准元素小,一部分大于等于基准元素。
此时基准元素在其排好序后的正确位置,然后再用同样的方法递归地排序划分的两部分。
实现
<?php
$arr = array(1,223,23,43,54,455,26,823,45,9,23,65);
/**
* [quickSort description]
* @param [type] $arr [description]
* @return [type] [description]
*/
function quickSort($arr){
//先判断是否需要继续进行
$len = count($arr);
if($len <= 1){
return $arr;
}
//选择第一个元素作为基准
$base_num = $arr[0];
//遍历除了标尺外的所有元素,按照大小关系放入两个数组内
//初始化两个数组
$left_array = array(); //小于基准值的数组
$right_array = array(); //大于基准的数组
for($i=1;$i<$len;$i++){
if($base_num > $arr[$i]){
//放入左边
$left_array[] = $arr[$i];
} else{
//放入右边
$right_array[] = $arr[$i];
}
}
//分别对左边和右边的数组进行相同的排序处理方式递归调用这个函数
$left_array = quickSort($left_array);
$right_array = quickSort($right_array);
//合并
return array_merge($left_array, array($base_num), $right_array);
}
var_dump(quickSort($arr));
归并排序
思路分析
采用分治法,将已有序的子序列合并,从而得到完全有序的序列.
实现
<?php
$arr = array(1,223,23,43,54,455,26,823,45,9,23,65);
/**
* [mergeSort description]
* @param [type] $arr [description]
* @return [type] [description]
*/
function mergeSort($arr){
$len = count($arr);
if($len < 2){
return $arr;
}
//获取中间参考点值
$middle = floor($len/2);
//取左边区间
$left = array_slice($arr, 0, $middle);
//取右边区间
$right = array_slice($arr, $middle);
//调用归并函数
return merge(mergeSort($left), mergeSort($right));
}
/**
* 归并函数
* @param [type] $left [description]
* @param [type] $right [description]
* @return [type] [description]
*/
function merge($left, $right){
$res = array();
while(count($left) > 0 && count($right) > 0){
if($left[0] <= $right[0]){
array_push($res, array_shift($left));
} else{
array_push($res, array_shift($right));
}
}
//解决$left遗留元素
while(count($left) > 0){
array_push($res, array_shift($left));
}
//解决$right遗留元素
while(count($right) > 0){
array_push($res, array_shift($right));
}
return $res;
}
var_dump(mergeSort($arr));
堆排序
- 思路分析
建堆,建堆是不断调整堆的过程,从len/2处开始调整,一直到第一个节点,此处len是堆中元素的个数。建堆的过程是线性的过程,从len/2到0处一直调用调整堆的过程,相当于o(h1)+o(h2)…+o(hlen/2) 其中h表示节点的深度,len/2表示节点的个数,这是一个求和的过程,结果是线性的O(n)。
调整堆:调整堆在构建堆的过程中会用到,而且在堆排序过程中也会用到。利用的思想是比较节点i和它的孩子节点left(i),right(i),选出三者最大(或者最小)者,如果最大(小)值不是节点i而是它的一个孩子节点,那边交互节点i和该节点,然后再调用调整堆过程,这是一个递归的过程。调整堆的过程时间复杂度与堆的深度有关系,是lgn的操作,因为是沿着深度方向进行调整的。
堆排序:堆排序是利用上面的两个过程来进行的。首先是根据元素构建堆。然后将堆的根节点取出(一般是与最后一个节点进行交换),将前面len-1个节点继续进行堆调整的过程,然后再将根节点取出,这样一直到所有节点都取出。堆排序过程的时间复杂度是O(nlgn)。因为建堆的时间复杂度是O(n)(调用一次);调整堆的时间复杂度是lgn,调用了n-1次,所以堆排序的时间复杂度是O(nlgn)
- 实现
<?php
$arr = array(1,223,23,43,54,455,26,823,45,9,23,65);
/**
* [heapSort description]
* @param [type] $arr [description]
* @return [type] [description]
*/
function heapSort($arr) {
#初始化大顶堆
initHeap($arr, 0, count($arr) - 1);
#开始交换首尾节点,并每次减少一个末尾节点再调整堆,直到剩下一个元素
for($end = count($arr) - 1; $end > 0; $end--) {
$temp = $arr[0];
$arr[0] = $arr[$end];
$arr[$end] = $temp;
ajustNodes($arr, 0, $end - 1);
}
return $arr;
}
/**
* 初始化大顶堆
* 初始化最大堆,从最后一个非叶子节点开始,最后一个非叶子节点编号为 数组长度/2 向下取整
* @param [type] $arr [description]
* @return [type] [description]
*/
function initHeap(&$arr) {
$len = count($arr);
for($start = floor($len / 2) - 1; $start >= 0; $start--) {
ajustNodes($arr, $start, $len - 1);
}
}
/**
* 调整节点
* @param [type] $arr 待调整数组
* @param [type] $start 调整的父节点坐标
* @param [type] $end 待调整数组结束节点坐标
* @return [type] [description]
*/
function ajustNodes(&$arr, $start, $end) {
$maxInx = $start;
$len = $end + 1; #待调整部分长度
$leftChildInx = ($start + 1) * 2 - 1; #左孩子坐标
$rightChildInx = ($start + 1) * 2; #右孩子坐标
#如果待调整部分有左孩子
if($leftChildInx + 1 <= $len) {
#获取最小节点坐标
if($arr[$maxInx] < $arr[$leftChildInx]) {
$maxInx = $leftChildInx;
}
#如果待调整部分有右子节点
if($rightChildInx + 1 <= $len) {
if($arr[$maxInx] < $arr[$rightChildInx]) {
$maxInx = $rightChildInx;
}
}
}
#交换父节点和最大节点
if($start != $maxInx) {
$temp = $arr[$start];
$arr[$start] = $arr[$maxInx];
$arr[$maxInx] = $temp;
#如果交换后的子节点还有子节点,继续调整
if(($maxInx + 1) * 2 <= $len) {
ajustNodes($arr, $maxInx, $end);
}
}
}
var_dump(heapSort($arr));
桶排序
思路分析
先将数组根据其值的大小放入到桶的相应位置,然后在按照顺序将元素从桶中取出。
实现
<?php
$arr = array(1,223,23,43,54,455,26,823,45,9,23,65);
/**
* [tongSort description]
* @param [type] $arr [description]
* @param [type] $max [description]
* @return [type] [description]
*/
function tongSort($arr, $max){
$len = count($arr);
//填充木桶
$tong = array();
for($i=0;$i<$max;$i++){
$tong[$i] = 0;
}
//开始标示木桶
for($i = 0; $i<$len; $i++){
$tong[$arr[$i]]++;
}
$res = array();
//开始从木桶中拿出数据
for($i = 0; $i< $max ; $i++){
if($tong[$i] > 0){
for($j = 1; $j <= $tong[$i]; $j++){ //这一行主要用来控制输出多个数
$res[] = $i;
}
}
}
return $res;
}
var_dump(tongSort($arr, 1000));
基数排序
思路分析
将所有待比较数值(正整数)统一为同样的数位长度,数位较短的数前面补零。
然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。
实现
<?php
$arr = array(1,223,23,43,54,455,26,823,45,9,23,65);
/**
* [countingSort description]
* @param [type] $arr [description]
* @param boolean $digit_num [description]
* @return [type] [description]
*/
function countingSort($arr, $digit_num = false) {
if ($digit_num !== false) { #如果参数$digit_num不为空,则根据元素的第$digit_num位数进行排序
for ($i = 0; $i < count($arr); $i++) {
$arr_temp[$i] = get_specific_digit($arr[$i], $digit_num);
}
} else {
$arr_temp = $arr;
}
$max = max($arr);
$time_arr = array(); #储存元素出现次数的数组
#初始化出现次数数组
for ($i = 0; $i <= $max; $i++) {
$time_arr[$i] = 0;
}
#统计每个元素出现次数
for ($i = 0; $i < count($arr_temp); $i++) {
$time_arr[$arr_temp[$i]]++;
}
#统计每个元素比其小或相等的元素出现次数
for ($i = 0; $i < count($time_arr) - 1; $i++) {
$time_arr[$i + 1] += $time_arr[$i];
}
#利用出现次数对数组进行排序
for($i = count($arr) - 1; $i >= 0; $i--) {
$sorted_arr[$time_arr[$arr_temp[$i]] - 1] = $arr[$i];
$time_arr[$arr_temp[$i]]--;
}
$arr = $sorted_arr;
ksort($arr); #忽略这次对key排序的效率损耗
return $arr;
}
/**
* 计算某个数的位数
* @param [type] $number [description]
* @return [type] [description]
*/
function get_digit($number) {
$i = 1;
while ($number >= pow(10, $i)) {
$i++;
}
return $i;
}
/**
* 获取某个数字的从个位算起的第i位数
* @param [type] $num [description]
* @param [type] $i [description]
* @return [type] [description]
*/
function get_specific_digit($num, $i) {
if ($num < pow(10, $i - 1)) {
return 0;
}
return floor($num % pow(10, $i) / pow(10, $i - 1));
}
/**
* 基数排序,以计数排序作为子排序过程
* @param [type] $arr [description]
* @return [type] [description]
*/
function radix_sort(&$arr) {
#先求出数组中最大的位数
$max = max($arr);
$max_digit = get_digit($max);
for ($i = 1; $i <= $max_digit; $i++) {
counting_sort($arr, $i);
}
}
var_dump(countingSort($arr));
希尔排序
思路分析:
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行依次直接插入排序。
实现
<?php
$arr = array(1,223,23,43,54,455,26,823,45,9,23,65);
/**
* [shellSort description]
* @param [type] $arr [description]
* @return [type] [description]
*/
function shellSort($arr){
$length=count($arr);
$h=1;
while($h<$length/3)
{
$h=3*$h+1;//设置间隔
}
while($h>=1)
{
for($i=$h; $i<$length; $i++)
{
for($j=$i; $j>=$h && $arr[$j]<$arr[$j-$h]; $j-=$h)
{
$temp =$arr[$j-$h];
$arr[$j-$h]=$arr[$j];
$arr[$j]=$temp;
}
}
$h=($h-1)/3;
}
return $arr;
}
var_dump(shellSort($arr));
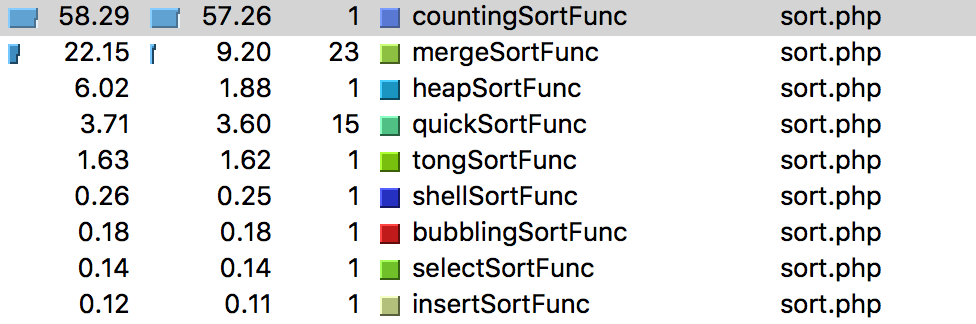
简单比较